MOVIMIENTO
DE PROYECTILES
Vamos
ahora a utilizar nuestros nuevos conocimientos para ver cómo
podemos describir el movimiento de un objeto que se lanza con una
determinada velocidad inicial en cualquier dirección.
Empecemos por el caso más simple de una bomba que se deja caer
desde un avión. En la figura podemos contemplar la trayectoria
de una bomba soltada desde un avión que vuela a 1000 m de
altura con una velocidad de 600 km/h.

Figura
5. Caída de una bomba desde una avión que vuela a 1000
m de altura con una velocidad de 600 km/h
¿Qué
cosas nos pueden interesar aquí?. Bueno, si usted fuera el
piloto del avión estaría interesado en cosas como el
lugar donde impactará el proyectil, cuánto tiempo
tardará en hacerlo y cosas por estilo. Nosotros somos aún
más curiosos y nos interesa también la velocidad que
lleva el proyectil en cualquier momento, la forma de la trayectoria y
todo lo relacionado con la posición del proyectil en cualquier
instante. Desde luego que somos bastante detallistas en esto de la
física y el lector podría pensar que se va a complicar
mucho el ejercicio de esa manera. Pero si hacemos el supuesto de
que los movimientos horizontal y vertical del proyectil se
pueden estudiar separadamente, todo empieza a hacerse más
sencillo.Parte horizontal del movimiento
Supongamos ahora que una vez soltado, el proyectil tiende a seguir llevando la misma velocidad que llevaba el avión y en la misma dirección. Pero el lector puede pensar: ¿cómo es esto?. El proyectil debería perder velocidad por dos razones:
- Por el rozamiento de aire
-
Porque
ya no hay ningún motor que lo impulse.
Movimiento vertical
El movimiento vertical se convierte en una simple caída libre de un objeto como ya hemos estudiado. La distancia vertical cubierta por el proyectil viene dada por la expresión 3 que en este caso se convierte en (ec. [6]):

Nuestro ejemplo en concreto
Vamos a empezar por calcular la distancia a la que impacta el proyectil. Estará de acuerdo el lector que esto ocurre cuando el proyectil haya caído los 1000 metros desde los que fue lanzado, es decir, que podemos sustituir en la ec 6

Nos preguntamos ahora con qué velocidad impacta el proyectil en el suelo. Aquí se nos presenta el problema de que tenemos una rapidez horizontal que sigue siendo de 167 m/s y una rapidez vertical que se calcula como:

Figura
6. Representación
del instante de impacto de la bomba contra el suelo.
Si
nos fijamos en la figura
6 podemos
ver como el truco para calcular la verdadera velocidad a partir de la
rapidez horizontal y vertical no es más que la aplicación
del teorema de Pitágoras a nuestro caso particular. Es decir,
tenemos que calcular el valor de la hipotenusa del triángulo
que se muestra en la figura
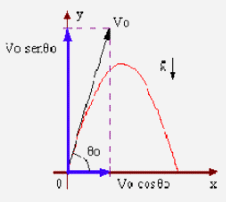
6 comoPor último me gustaría señalar el tipo de curva que sigue un proyectil en su movimiento. Todos hemos oído en la retransmisión de un partido de fútbol al locutor diciendo aquello de: "el balón describe una bonita parábola". La parábola es una curva matemática que se obtiene fácilmente si uno coge en un eje horizontal y pinta marcas igualmente espaciadas y en un eje vertical donde pinta rayas espaciadas cantidades que se multiplican sucesivamente por 1,4,9,16... veces la unida elegida. Esto es, según los cuadrados de los enteros. De forma general una parábola es una curva que relaciona la distancia vertical y con distancia horizontal x de la forma
Para ver que efectivamente nuestro proyectil sigue una curva de este tipo solamente tenemos que eliminar el tiempo t de las ecuaciones 5 , 6 y obtener una relación entre la distancia recorrida verticalmente y la cubierta horizontalmente. Quede esto como ejercicio para los lectores más interesados en la matemática del asunto.
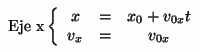




![$\displaystyle r=\frac{n\sum x_{i}y_{i}-\sum x_{i} \sum y_{i}}{\sqrt{[n\sumx_{i}^{2}-(\sum x_{i})^2][n\sum y_{i}^2-(\sum y_{i})^2]}} .$](http://www.lawebdefisica.com/apuntsfis/errores/img35.png)