TRATAMIENTO
DE ERRORES
Tratamiento de errores
En
física se estudian diferentes modelos matemáticos que
intentan explicar de modo aproximado cómo se comporta la
naturaleza e intentar predecir las consecuencias en determinados
experimentos. Si el modelo no falla en sus predicciones se va
consolidando poco a poco en la teoría física. Sin
embargo, desde el momento en el que falla se debe abandonar o, como
mucho, limitar su aplicabilidad.
Sin
embargo también pueden ser los experimentos los que fallen. No
quiero decir, por supuesto, que la naturaleza se confunda y en vez de
haber gravedad atractiva veamos como, al soltar una bolita, ésta
escapa de la Tierra. Me refiero a que, cuando tomamos datos en un
experimento, estos datos presentan cierta incertidumbre.
Cuando
medimos una distancia con una regla milimetrada puede ocurrir que la
distancia esté justo entre dos marcas del milímetro. Si
medimos un voltaje con un polímetro podemos ver que este
oscile entre dos valores. Por tanto, cada medida viene con un error
intrínseco que en general se escribe como
Estos
errores se tienen que tratar a la hora de realizar los informes de
los experimentos y propagarlos a las cantidades que querramos
determinar a partir de ellos. Por ejemplo, con una regla y un
cronómetro podemos medir la distancia que recorrió un
objeto y el tiempo que tardó, pero no medimos directamente su
velocidad, por lo que el error en la velocidad vendrá dada a
partir del error en la distancia y el error en el tiempo.
Tipos de errores
Básicamente
hay tres tipos de errores diferentes:
- Sistemáticos: Estos errores vienen, como su nombre indica, por sistema. Puede que empleemos una regla mal graduada en que cada centímetro mida en realidad 13 milímetros, o puede que nos hayamos olvidado de sumar el diámetro de una bola a la hora de marcar la distancia entre la bola y un punto. Estos errores hay que intentar evitarlos y, en caso de cometerlos, darse cuenta a tiempo. Generalmente el valor verdadero de la magnitud a medir no se encuentra en la región de los datos tomados.
- Estadísticos: Estos errores vienen dados por motivos muy diversos. En este caso el valor verdadero de la magnitud a medir está en la región de los datos tomados.
- Incertidumbres: Estos errores son causados por la precisión del aparato que empleamos para medir, que puede ser menor o igual a las fluctuaciones estadísticas de la medida.
Cifras significativas. Notación científica
Las
cifras significativas son aquellas que aportan información
útil en un número. Las cifras no significativas son las
que aparecen como resultados del cálculo. Se consideran cifras
significativas aquellas que tienen igual o mayor peso que el error de
un número. Por ejemplo, si tenemos la magnitud
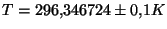 las cifras a partir de la centésima de kelvin (incluída
ésta) no aportan nada nuevo, pues son de mucha menor magnitud
que el error y entran dentro de las fluctuaciones. También se
considera que los ceros no son cifras significativas, excepto cuando
estén entre dos cifras distintas de cero. Por ejemplo
las cifras a partir de la centésima de kelvin (incluída
ésta) no aportan nada nuevo, pues son de mucha menor magnitud
que el error y entran dentro de las fluctuaciones. También se
considera que los ceros no son cifras significativas, excepto cuando
estén entre dos cifras distintas de cero. Por ejemplo
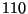 tiene dos cifras significativas,
tiene dos cifras significativas,
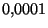 tiene una cifra significativa, pero
tiene una cifra significativa, pero
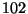 tiene tres.
tiene tres.
Esto
se suele resolver empleando notación científico. En
estos tres últimos casos, en notación científica
escribimos
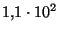 ,
,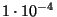 y
y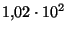 .
Como vemos el número de cifras significativas en notación
científica es trivial.
.
Como vemos el número de cifras significativas en notación
científica es trivial.
Hay
que hacer notar que la medida se tiene que dar hasta el peso del
error. Supongamos que tenemos una medida
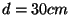 con un error de un milímetro, en ese caso se debe escribir
con un error de un milímetro, en ese caso se debe escribir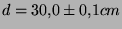 .
.
Redondeo de números
Por
tanto, cuando tenemos cifras no significativas hay que eliminarlas,
pero no simplemente borrándoles, sino redondeando. Es obvio
que si tenemos que redondear
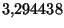 a la primera cifra decimal es mucho más correcto escribir
a la primera cifra decimal es mucho más correcto escribir
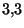 que
que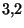 .
Generalmente se dan las siguientes reglas de redondeo:
.
Generalmente se dan las siguientes reglas de redondeo:
- Si la cifra que se omite es menor que 5, la eliminación se realiza sin más.
- Si la cifra que se omite es mayor que 5, se aumenta en una unidad la última cifra que se conserva.
- Si la cifra que se omite es 5 se elimina si la última cifra retenida es par y se suma uno a la última cifra retenida si es impar
Por
supuesto, en el último punto también existe el convenio
contrario. Estadística mente son equivalentes.
Especificación de incertidumbres
Ya
hemos visto que, en general, el error de un número se escribe
como
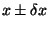 ,
con
,
con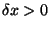 .
Se considera que el valor verdadero de la magnitud debería
estar entre
.
Se considera que el valor verdadero de la magnitud debería
estar entre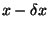 y
y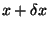 .
.
Si
lo que queremos es comparar dos medidas con errores diferentes para
ver cuál es más precisa usamos el error relativo, que
es el cociente entre el error y la medida, de modo que cuanto menor
sea este error relativo más precisa será la medida.
Para dar el error en porcentaje de la medida no hay más que
multiplicar el error relativo por cien.
Asignación del error
Ahora
lo que hay que saber es cómo se asigna un error, caben dos
posibilidades, que las medidas sean directas (como medir distancias
con una regla o el tiempo con un cronómetro) o, por el
contrario, indirectas (como medir la resistencia que presenta un
circuito y calcular la intensidad de la corriente).
Medidas directas
Cuando
las medidas son directas vuelve a haber dos posibilidades, que se
halla realizado una sola medida o que se hayan realizado varias.
Si
se realiza una sola medida el error que se asigna es la sensibilidad
del objeto que se use para medir (si es una regla graduada en
milímetros el error será de un milímetro), o
bien un error tal que recoja las fluctuaciones del objeto con la que
se está midiendo.
Si
se realizan
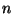 medidas se empleará como valor real la media aritmética
de todas ellas:
medidas se empleará como valor real la media aritmética
de todas ellas:
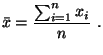
Y
para el error se empleará la desviación típica
del valor medio:
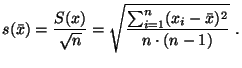
Medidas indirectas
Para
calcular medidas indirectas que son función de otras (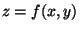 )
se actuará de la siguiente manera.
)
se actuará de la siguiente manera.
El
valor de la medida no será otro que la solución a la
función, y el valor del error se calculará según
las siguientes expresiones:
Si
las variables fueron medidas una sola vez:
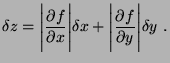
Y
si las variables fueron medidas varias veces:
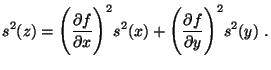
Medias ponderadas
Cuando
tenemos varias medias de un mismo valor con sus respectivos errores
podemos calcular un valor con su error de manera que tengan más
peso los valores más precisos mediante la fórmula:
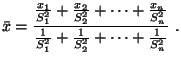
Y
su error vendrá dado por:
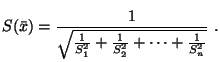
Ajuste a una recta
En
ocasiones querremos representar los datos que tenemos y hallar la
función que describe su comportamiento. Cuando esta función
es una recta de la forma
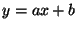 se emplea el Método de los Mínimos Cuadrados, que nos
da el valor de los coeficientes
se emplea el Método de los Mínimos Cuadrados, que nos
da el valor de los coeficientes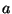 y
y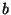 con su error, de este modo:
con su error, de este modo:
|
|
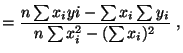 |
(1)
|
|
|
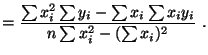 |
(2)
|
Para
medir la calidad de este ajuste, es decir, si los datos están
más o menos cerca de los valores teóricos que nos da la
recta calculada, se emplea el coeficiente de correlación, que
está acotado entre
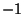 y
y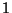 . Este coeficiente es tanto mejor cuanto más se acerque a
alguno de estos valores y peor cuanto más se acerque a cero.
La fórmula de coeficiente de correlación es:
. Este coeficiente es tanto mejor cuanto más se acerque a
alguno de estos valores y peor cuanto más se acerque a cero.
La fórmula de coeficiente de correlación es:
![$\displaystyle r=\frac{n\sum x_{i}y_{i}-\sum x_{i} \sum y_{i}}{\sqrt{[n\sumx_{i}^{2}-(\sum x_{i})^2][n\sum y_{i}^2-(\sum y_{i})^2]}} .$](http://www.lawebdefisica.com/apuntsfis/errores/img35.png)
No hay comentarios:
Publicar un comentario