MOVIMIENTO DE LOS CUERPOS EN DOS DIMENSIONES

MOVIMIENTO DE TRAYECTORIA BIDIMENSIONAL

TIRO PARABÓLICO

Objetivo: Adquirir conocimiento sobre el tiro parabólico y la aplicación de formulas para la resolución de problemas.

Introducción

El tiro oblicuo es un caso de composición de dos movimientos perpendiculares, uno rectilíneo y uniforme(MRU) sobre el eje X y otro rectilíneo uniformemente variado(MRUV) sobre el eje Y. A partir de las ecuaciones de posición, velocidad y de la ecuación de la trayectoria(parábola) se resuelven todas las situaciones posibles(prescindiendo del rozamiento con el aire).

Los Vuelos parabólicos se usan desde muchos años con regularidad para obtener por un tiempo corto condiciones sin gravedad. Esto sirve para el entrenamiento de astronautas pero también para probar equipo en condiciones de ausencia de gravedad. Nótese, que la gravedad de hecho no es ausente sonó compensado por fuerzas virtuales del vuelo parabólico.

Esto es según yo se la única aplicación del vuelo parabólico, porque las trayectorias de ifles o cánones no son realmente parabólicas debido a la fricción del proyectil en el aire. Por ende la parábola es una aproximación muy burda que no sirve para calcular trayectorias de artillería. Entonces porque existen vuelos parabólicos en la atmósfera? La razón es que los motores del avión pueden compensar las pérdidas por fricción en forma muy exacta.

¿A que se le denomina tiro parabólico?

Se denomina tiro parabólico, en general, a aquellos movimientos que suceden de forma bidimensional sobre la superficie de la tierra.

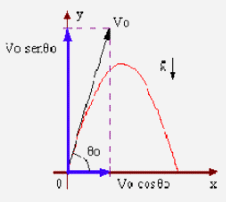
Para este tipo de móviles el movimiento se descompone en sus componentes X e Y. El movimiento en X no sufre aceleración, y por tanto sus ecuaciones serán

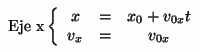
pero enh cambio en el eje Y se deja sentir la fuerza de la gravedad, supuesta constante y por tanto sus ecuaciones serán

Algunas preguntas típicas del tiro parabólico son calcular el alcance y altura máxima. Estas preguntas se pueden contestar sabiendo que la altura máxima se alcanzará cuando. De esta condición se extrae el tiempo que tarda en alcanzar la altura máxima y sustituyendo en la ecuación de las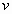se obtiene la altura máxima. El alcance máximo se puede calcular razonando que, para cuando esto suceda, el móvil volverá estar al nivel del suelo y por tanto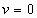, sustituyendo se obtiene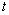y, sustituyendo éste en las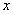el resultado. Otras cantidades se pueden conseguir de manera similar.